Измерить алгеброй гармонию

Измерить алгеброй гармонию
Всегда считалось, что гармонию невозможно измерить алгебру. Но в последнее время с развитием математики, техники и человеческого воображения, этот стереотип активно разрушается. К примеру, американский фотограф и математик Никки Грациано (Nikki Graziano) любит находить функции, соответствующие тому или иному явлению природы.

Измерить алгеброй гармонию

Измерить алгеброй гармонию
Никки Грационо учится в Рочестерском Технологическом Институте (Rochester Institute of Technology) в штате Нью-Йорк на математическом отделении. А параллельно занимается фотографией. Вот он и решил объединить эти два своих главнейших занятия в жизни.

Измерить алгеброй гармонию

Измерить алгеброй гармонию
Он давно замечал, что многие природные очертания можно описать функциями. От этого понимания достаточно было сделать всего один шаг, чтобы прийти к художественному методу, которым сейчас Никки Грациано пользуется в своем творчестве.
Измерить алгеброй гармонию

Измерить алгеброй гармонию
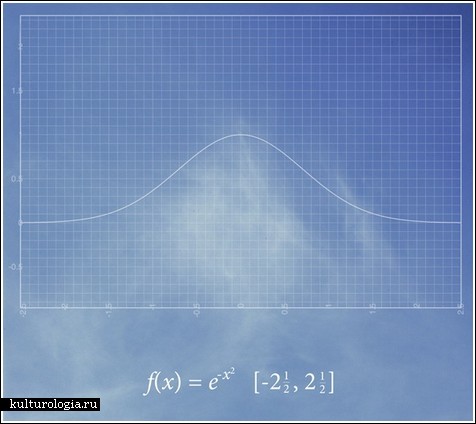
Он накладывает изображения функций с их описанием на фотографии живой природы. Это может быть дерево или заросли кустарника, это могут быть облака в небе или тень на земле. Это могут быть большие, укрытые снегом горные гряды или песчаные барханы. Везде в природе, по утверждению Никки Грациано, помимо гармонии, есть и алгебра. Нужно только ее найти.



